Coupled DAE Problems
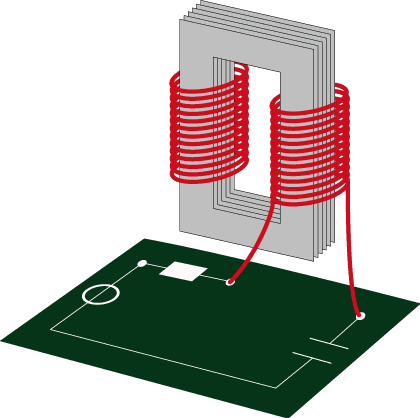
A circuit (DAE model) coupled to a magnetostatic field device (PDE model)
Coupled Problems of differential-algebraic equations (DAEs) arise typically from either multiphysical modeling (e.g. in circuit simulation with heating) or from refined modeling, where crucial parts of the original problem are replaced by a better, but computational more expensive model (e.g. circuits refined by field models). Furthermore splitting methods may turn a monolithic DAE problem into coupled subproblems, e.g. because of different time scales (multirate). In any case the DAEs arise from network approaches or space-discretization of PDAEs (Partial Differential Algebraic Equations).
Often the coupled equations have quite different properties, i.e., symmetries, definiteness or time scales. Thus the coupled system must be analyzed (e.g. the index) and tailored methods have to be developed (e.g. dynamic iteration).
Details
Publications
- 2015
3117.
Mathematical Modelling and Numerical Simulation of Oil Pollution Problems
In Ehrhardt, Matthias, Editor aus The Reacting Atmosphere
Herausgeber: Springer Cham
2015ISBN: 978-3-319-16458-8
3116.
Tausch, Michael W.
Mehr Licht! Auch im Chemieunterricht!
{CHEMKON}, 22 (4) :161--161
2015
Herausgeber: Wiley3115.
Bredenkamp, Angela; Zhu, Zhi-Bin; Häring, Andreas P.
Method for producing chiral compounds
Mai 20153114.
Bolten, Matthias; Gottschalk, H.; Schmitz, S.
Minimal failure probability for ceramic design via shape control
J. Optim. Theory Appl., 166 :983-1001
20153113.
Bolten, M.; Gottschalk, H.; Schmitz, S.
Minimal failure probability for ceramic design via shape control
J. Optim. Theory Appl., 166 :983-1001
20153112.
Bolten, M.; Gottschalk, H.; Schmitz, S.
Minimal failure probability for ceramic design via shape control
J. Optim. Theory Appl., 166 :983---1001
20153111.
Striebel, M.; Pulch, R.; Maten, E. J. W.; Ilievski, Z.; Schilders, W. H. A.
Model order reduction and sensitivity analysis
In Günther, M., Editor, Coupled Multiscale Simulation and Optimization in Nanoelectronics Band 21 aus Mathematics in Industry
Kapitel 5.3, Seite 319--341 and 355--358
Herausgeber: Springer
2015
319--341 and 355--3583110.
Striebel, M.; Maten, E. J. W.
Model order reduction for nonlinear network problems
In Günther, M., Editor, Coupled Multiscale Simulation and Optimization in Nanoelectronics Band 21 aus Mathematics in Industry
Kapitel 6.1, Seite 362-380 and 426-428
Herausgeber: Springer
2015
362-380 and 426-4283109.
Antoulas, Athanasios C.; Ionutiu, Roxana; Martins, Nelson; Maten, E. Jan W.; Mohaghegh, Kasra; Pulch, Roland; Rommes, Joost; Saadvandi, Maryam; Striebel, Michael
Model order reduction: Methods, concepts and properties
In Günther, Michael, Editor
Seite 159–265
Herausgeber: Springer Berlin Heidelberg
2015
159–2653108.
Antoulas, Athanasios C.; Ionutiu, Roxana; Martins, Nelson; Maten, E. Jan W.; Mohaghegh, Kasra; Pulch, Roland; Rommes, Joost; Saadvandi, Maryam; Striebel, Michael
Model Order Reduction: Methods, Concepts and Properties
In Günther, M., Editor, Coupled Multiscale Simulation and Optimization in Nanoelectronics Band 21 aus Mathematics in Industry
Kapitel 4, Seite 159--265
Herausgeber: Springer
2015
159--2653107.
Antoulas, Athanasios C.; Ionutiu, Roxana; Martins, Nelson; Maten, E. Jan W.; Mohaghegh, Kasra; Pulch, Roland; Rommes, Joost; Saadvandi, Maryam; Striebel, Michael
Model order reduction: Methods, concepts and properties
In Günther, Michael, Editor
Seite 159–265
Herausgeber: Springer Berlin Heidelberg
2015
159–2653106.
Teng, Long; Emmerich, Cathrin; Ehrhardt, Matthias; G\"unther, Michael
Modelling Stochastic Correlation with modified {Ornstein-Uhlenbeck} process
ECMI book subseries of Mathematics in Industry
18th European Conference on Mathematics for Industry, Taormina, Italy
Herausgeber: Springer, Heidelberg
20153105.
Mohaghegh, K.; Pulch, R.; Maten, E. J. W.
MOR for singularly perturbed systems
In Günther, M., Editor, Coupled Multiscale Simulation and Optimization in Nanoelectronics Band 21 aus Mathematics in Industry
Kapitel 5.4, Seite 341--351 and 358--359
Herausgeber: Springer
2015
341--351 and 358--3593104.
Putek, Piotr; PAPLICKI, Piotr; Pulch, Roland; Maten, E. Jan W.; Günther, Michael; Palka, Ryszard
Multi-objective topology optimization and losses reduction in a permanent magnet excited synchronous machine
Preprint IMACM :1–10
2015
Herausgeber: Bergische Universität Wuppertal3103.
Putek, Piotr; PAPLICKI, Piotr; Pulch, Roland; Maten, E. Jan W.; Günther, Michael; Palka, Ryszard
Multi-objective topology optimization and losses reduction in a permanent magnet excited synchronous machine
Preprint IMACM :1–10
2015
Herausgeber: Bergische Universität Wuppertal3102.
Putek, Piotr; PAPLICKI, Piotr; Pulch, Roland; Maten, Jan; Günther, Michael; PA{\L}KA, Ryszard
Multi-objective topology optimization and losses reduction in a permanent magnet excited synchronous machine
20153101.
Maten, E. Jan W.; Putek, Piotr; Günther, Michael; Tischendorf, Caren; Strohm, Christian; Schoenmaker, Wim; Meuris, Peter; Smedt, Bart De; Benner, Peter; Feng, Lihong; Banagaaya, Nicodemus; Yue, Yao; Janssen, Rick; Dohmen, Jos J.; Tasic, Bratislav; others
Nanoelectronic COupled Problems Solutions - nanoCOPS
Preprint IMACM
2015
Herausgeber: Bergische Universität Wuppertal3100.
Maten, E. Jan W.; Putek, Piotr; Günther, Michael; Tischendorf, Caren; Strohm, Christian; Schoenmaker, Wim; Meuris, Peter; Smedt, Bart De; Benner, Peter; Feng, Lihong; Banagaaya, Nicodemus; Yue, Yao; Janssen, Rick; Dohmen, Jos J.; Tasic, Bratislav; others
Nanoelectronic COupled Problems Solutions - nanoCOPS
Preprint IMACM
2015
Herausgeber: Bergische Universität Wuppertal3099.
Maten, E Jan W; Putek, Piotr; Günther, Michael; Tischendorf, Caren; Strohm, Christian; Schoenmaker, Wim; Meuris, Peter; De Smedt, Bart; Benner, Peter; Feng, Lihong; others
Nanoelectronic COupled Problems Solutions-nanoCOPS
20153098.
Heucken, Carmen Monika
Neuartige Tenside/polymertenside auf Basis von Zitronensäure
20153097.
Hanebaum, Sonja
Oberflächenaktive Substanzen auf Basis von Citronensäure
20153096.
Petrov, P.; Ehrhardt, M.
On Mayfield's stability proof for the discretized transparent boundary condition for the parabolic equation
Appl. Math. Lett., 44 :45--49
20153095.
Ehrhardt, Matthias
On Mayfield’s stability proof for the discretized transparent boundary condition for the parabolic equation
Applied Mathematics Letters, 44 :45--49
2015
Herausgeber: Pergamon3094.
Ehrhardt, Matthias
On Mayfield’s stability proof for the discretized transparent boundary condition for the parabolic equation
Applied Mathematics Letters, 44 :45–49
2015
Herausgeber: Pergamon3093.
Ehrhardt, Matthias
On Mayfield’s stability proof for the discretized transparent boundary condition for the parabolic equation
Applied Mathematics Letters, 44 :45–49
2015
Herausgeber: Pergamon
