Positivity Perserving Discretizations
In the process of modelling and simulation of physical phenomena, it is desirable that numerical quantities reflect the original physical behaviour. This also holds true in electrical engineering.
Charge transport in semiconductor devices, for instance, is often described by convection-diffusion type problems, i.e. elliptic-parabolic PDEs. Thereby the charge transport is described in terms of charge carrier densities, which - by their physical - meaning should be non-negative. Even if the analytical solution of the problem equations would remain non-negative, this can in general not be ensured for the final simulation result, since this property may be lost within the process of space discretization or time integration. This leads us to the following research topics:
- Positivity preserving space discretization of certain convection-diffusion-type problems
- Positivity preserving time integration for space discretized semiconductor model equations
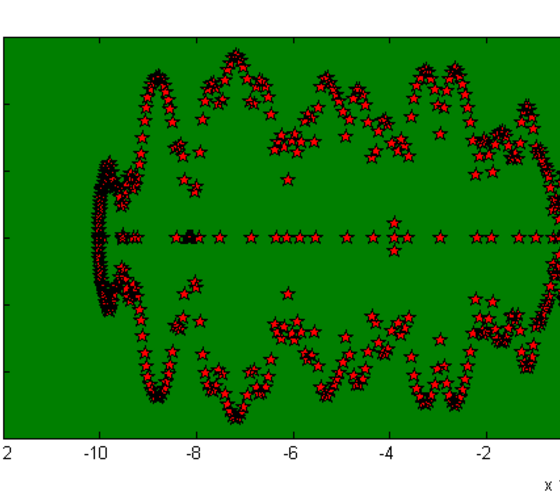
Eigenvalues of a typical mass-matrix for the semiconductor problem
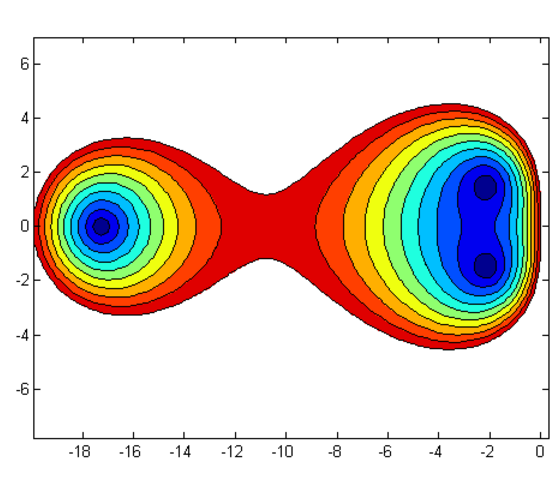
Stability domain of a useful time integration method
Cooperations
- Anne Kvaernoe, NTNU Trondheim
