Dynamic Iteration Schemes
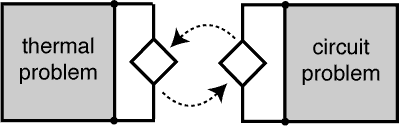
Dynamic iteration via source coupling
Standard time-integration methods solve transient problems all at once. This may become very inefficient or impossible for large systems of equations. Imaging that such large systems often stem from a coupled problem formulation, where different physical phenomena interact and need to be coupled in order to produce a precise mathematical model.
E.g. highly integrated electric circuits (as in memory chips or CPUs) produce heat, which effects in turn their behavior as electrical system; thus one needs to couple electric and thermal subproblem descriptions. On the one hand, this creates multiple time scales due to different physical phenomena, which demands an efficient treatment, see multirate. On the other hand, in a professional environment one usually has dedicated solvers for the subproblems, which need to be used, and an overall problem formulation is not feasible for any of the involved tools.
For those partitioned problems a dynamic iteration method becomes beneficial or even the sole way-out: it keeps the subproblems separate, solves subproblems sequentially (or in parallel) and iterates until convergence (fixed-point interation). Thus the subproblem's structure can be exploited in the respective integration.
To guarantee or to speed up convergence the time interval of interest is split into a series of windows. Then the time-integration of the windows is applied sequentially and in each window the subproblems are solved iteratively by your favoured method.
Group members working on that field
- Andreas Bartel
- Michael Günther
Former and ongoing Projects
Cooperation
- Herbert De Gersem, Katholieke Universiteit Leuven
Publications
- 2024
5303.
Vinod, Vivin; Kleinekathöfer, Ulrich; Zaspel, Peter
Optimized multifidelity machine learning for quantum chemistry
Mach. Learn.: Sci. Technol., 5 (1) :015054
20245302.
Frommer, Andreas; Ramirez-Hidalgo, Gustavo; Schweitzer, Marcel; Tsolakis, Manuel
Polynomial preconditioning for the action of the matrix square root and inverse square root
Electron. Trans. Numer. Anal., 60 :381-404
20245301.
Jacob, B.; Totzeck, Claudia
Port-Hamiltonian Structure of Interacting Particle Systems and Its Mean-Field Limit
SIAM Multiscale Modelling & Simulation, 22
20245300.
Bartel, A.; Clemens, M.; Günther, M.; Jacob, Birgit; Reis, T.
Port-Hamiltonian Systems Modelling in Electrical Engineering
Band 43
Herausgeber: Springer, Cham.
van Beurden, M., Budko, N.V., Ciuprina, G., Schilders, W., Bansal, H., Barbulescu, R. Edition
20245299.
Bartel, Andreas; Clemens, Markus; Günther, Michael; Jacob, Birgit; Reis, Timo
Port-Hamiltonian systems’ modelling in electrical engineering
In van Beurden, Martijn and Budko, Neil V. and Ciuprina, Gabriela and Schilders, Wil and Bansal, Harshit and Barbulescu, Ruxandra, Editor, Scientific Computing in Electrical Engineering: SCEE 2022, Amsterdam, The Netherlands, July 2022ausMathematics in Industry, Seite 133–143
In van Beurden, Martijn and Budko, Neil V. and Ciuprina, Gabriela and Schilders, Wil and Bansal, Harshit and Barbulescu, Ruxandra, Editor
Herausgeber: Springer Cham
20245298.
Bartel, Andreas; Clemens, Markus; Günther, Michael; Jacob, Birgit; Reis, Timo
Port-Hamiltonian systems’ modelling in electrical engineering
In van Beurden, Martijn and Budko, Neil V. and Ciuprina, Gabriela and Schilders, Wil and Bansal, Harshit and Barbulescu, Ruxandra, Editor, Scientific Computing in Electrical Engineering: SCEE 2022, Amsterdam, The Netherlands, July 2022ausMathematics in Industry, Seite 133–143
In van Beurden, Martijn and Budko, Neil V. and Ciuprina, Gabriela and Schilders, Wil and Bansal, Harshit and Barbulescu, Ruxandra, Editor
Herausgeber: Springer Cham
20245297.
Vinod, Vivin; Lyu, Dongyu; Ruth, Marcel; Kleinekathöfer, Ulrich; Schreiner, Peter R.; Zaspel, Peter
Predicting Molecular Energies of Small Organic Molecules with Multifidelity Methods.
20245296.
Ackermann, Julia; Kruse, Thomas; Urusov, Mikhail
Reducing Obizhaeva-Wang-type trade execution problems to LQ stochastic control problems
Finance and Stochastics, 28 (3) :813–863
2024
Herausgeber: Springer Verlag5295.
Ackermann, Julia; Kruse, Thomas; Urusov, Mikhail
Reducing Obizhaeva-Wang-type trade execution problems to LQ stochastic control problems
Finance and Stochastics, 28 (3) :813–863
2024
Herausgeber: Springer Verlag5294.
Saini, B. S.; Miettinen, K.; Klamroth, Kathrin; Steuer, R. E.; Dächert, Kerstin
SCORE Band Visualizations: Supporting Decision Makers in Comparing High-Dimensional Outcome Vectors in Multiobjective Optimization
IEEE Access, 12 :164371—164388
20245293.
Ackermann, Julia; Kruse, Thomas; Urusov, Mikhail
Self-exciting price impact via negative resilience in stochastic order books
Annals of Operations Research, 336 (1) :637–659
2024
Herausgeber: Springer Netherlands5292.
Ackermann, Julia; Kruse, Thomas; Urusov, Mikhail
Self-exciting price impact via negative resilience in stochastic order books
Annals of Operations Research, 336 (1) :637–659
2024
Herausgeber: Springer Netherlands5291.
Andersen, Kim Allan; Boomsma, Trine Krogh; Efkes, Britta; Forget, Nicolas
Sensitivity Analysis of the Cost Coefficients in Multiobjective Integer Linear Optimization
Management Science
20245290.
Palitta, Davide; Schweitzer, Marcel; Simoncini, Valeria
Sketched and truncated polynomial Krylov subspace methods: Matrix Sylvester equations
Math. Comp.
20245289.
Hastir, Anthony; Jacob, Birgit; Zwart, Hans
Spectral analysis of a class of linear hyperbolic partial differential equations
IEEE Control Systems Letters, 8 :766-771
20245288.
Bartel, Andreas; Diab, Malak; Frommer, Andreas; Günther, Michael; Marheineke, Nicole
Splitting Techniques for DAEs with port-Hamiltonian Applications
Preprint
20245287.
Bartel, Andreas; Diab, Malak; Frommer, Andreas; Günther, Michael; Marheineke, Nicole
Splitting Techniques for DAEs with port-Hamiltonian Applications
Preprint
20245286.
Bartel, A.; Diab, M.; Frommer, A.; G\"unther ; Marheineke, N.
Splitting Techniques for DAEs with port-Hamiltonian Applications
20245285.
Sprachsensibler Chemieunterricht digital umgesetzt - Ein Seminarexkurs im Rahmen des Praxissemesters
20245284.
Ackermann, Julia; Ehrhardt, Matthias; Kruse, Thomas; Tordeux, Antoine
Stabilisation of stochastic single-file dynamics using port-Hamiltonian systems
arXiv preprint arXiv:2401.17954
20245283.
Ackermann, Julia; Ehrhardt, Matthias; Kruse, Thomas; Tordeux, Antoine
Stabilisation of stochastic single-file dynamics using port-Hamiltonian systems
Preprint
20245282.
Ackermann, Julia; Ehrhardt, Matthias; Kruse, Thomas; Tordeux, Antoine
Stabilisation of stochastic single-file dynamics using port-Hamiltonian systems
Preprint
20245281.
Ackermann, Julia; Ehrhardt, Matthias; Kruse, Thomas; Tordeux, Antoine
Stabilisation of stochastic single-file dynamics using port-Hamiltonian systems
Preprint
20245280.
Jacob, Birgit; Glück, Jochen; Meyer, Annika; Wyss, Christian; Zwart, Hans
Stability via closure relations with applications to dissipative and port-Hamiltonian systems
J. Evol. Equ., 24 :Paper No. 62
20245279.
Clemens, Markus; Henkel, Marvin-Lucas; Kasolis, Fotios; Günther, Michael
Structural Aspects of Electromagneto-Quasistatic Field Formulations of Darwin-Type Derived in the Port-Hamiltonian System Framework
TechRxiv
2024
Herausgeber: IEEE
