Coupled DAE Problems
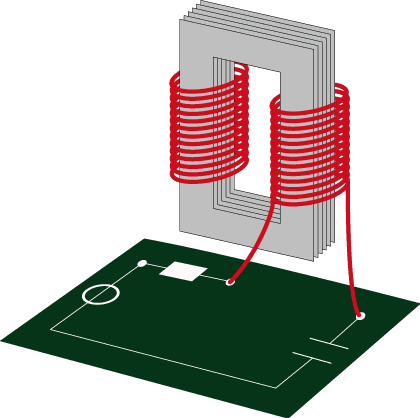
A circuit (DAE model) coupled to a magnetostatic field device (PDE model)
Coupled Problems of differential-algebraic equations (DAEs) arise typically from either multiphysical modeling (e.g. in circuit simulation with heating) or from refined modeling, where crucial parts of the original problem are replaced by a better, but computational more expensive model (e.g. circuits refined by field models). Furthermore splitting methods may turn a monolithic DAE problem into coupled subproblems, e.g. because of different time scales (multirate). In any case the DAEs arise from network approaches or space-discretization of PDAEs (Partial Differential Algebraic Equations).
Often the coupled equations have quite different properties, i.e., symmetries, definiteness or time scales. Thus the coupled system must be analyzed (e.g. the index) and tailored methods have to be developed (e.g. dynamic iteration).
Details
Publications
- 2025
5443.
Sinani, Mario; Wynn, Andrew; Palacios, Rafael
Physics-Informed Data-Driven Modelling of Nonlinear Aerodynamic Forces of the Pazy Wing
AIAA SciTech Forum, 6-10 January
Januar 20255442.
Vinod, Vivin; Lyu, Dongyu; Ruth, Marcel; R. Schreiner, Peter; Kleinekathöfer, Ulrich; Zaspel, Peter
Predicting Molecular Energies of Small Organic Molecules With Multi-Fidelity Methods
J. Comp. Chem., 46 (6) :e70056
20255441.
[german] Zeller, Diana; Bohrmann-Linde, Claudia; Mack, Nils; Schrader, Claudia
Produktion eigener VR-Lernsettings im Projekt FoPro-VR. Ein interdisziplinärer Lehransatz für die Lehramtsausbildung
In Mrohs, Lorenz; Franz, Julia; Herrmann, Dominik; Lindner, Konstantin; Staake, Thorsten, Editor, Digitales Lehren und Lernen an der Hochschule. Strategien - Bedingungen - Umsetzung
Seite 191-204
Herausgeber: transcript, Bielefeld
2025
191-204ISBN: 9783839471203
5440.
Khosrawi-Rad, Bijan; Keller, Paul; Benner, Dennis; Grogorick, Linda; Borchers, Arne; Janson, Andreas; Leimeister, Jan Marco; Robra-Bissantz, Susanne
Promoting Students’ Motivation in Language Education with Gamified Pedagogical Conversational Agents
Computers & Education, 238 :1–24
20255439.
Vinod, Vivin; Zaspel, Peter
QeMFi: A Multifidelity Dataset of Quantum Chemical Properties of Diverse Molecules
Sci. Data, 12 (1) :202
2025
Herausgeber: Nature Publishing Group
ISSN: 2052-44635438.
Patel, Vivak; Maldonado, D Adrian; Melnichenko, Maksim; Pritchard, Nathaniel; Rao, Vishwas; Rebrova, Elizaveta; Sankararaman, Sriram; Schweitzer, Marcel
Scientific Applications Leveraging Randomized Linear Algebra
20255437.
Clément, François; Doerr, Carola; Klamroth, Kathrin; Paquete, Luís
Searching Permutations for Constructing Uniformly Distributed Point Sets
Proceedings of the National Academy of Sciences, 122 (14) :e2424464122
20255436.
Palitta, Davide; Schweitzer, Marcel; Simoncini, Valeria
Sketched and truncated polynomial Krylov methods: Evaluation of matrix functions
Numer. Linear Algebra Appl., 32 :e2596
20255435.
Arora, Sahiba; Mui, Jonathan
Smoothing of operator semigroups under relatively bounded perturbations
20255434.
Santos, Daniela Dos; Klamroth, Kathrin; Martins, Pedro; Paquete, Luís
Solving the Multiobejctive Quasi-Clique Problem
European Journal of Operational Research, 323 :409—424
20255433.
Gökkus, Yasemin
Spieleentwickung im Chemieunterricht. Auftakt einer Aktionsforschung
MNU-Journal, 03/2025 :182-190
20255432.
Hamadi, Majed; Mahdavi-Amiri, Nezam; Schweitzer, Marcel
Splitting methods based on the nonzero diagonal pattern for computing matrix functions
20255431.
[german] Zeller, Diana; Ramella, Abigail; Mack, Nils; Schrader, Claudia; Bohrmann-Linde, Claudia
Virtual Reality im Unterricht – Potentiale und Herausforderungen beim Einsatz von VR im Chemieunterricht
MNU-Journal, 04/2025 :284-289
20255430.
[german] Kiesling, Elisabeth; Bohrmann-Linde, Claudia
Von der Leitlinie BNE zum bilingual-englischen Schülerlabor- Konzeption, Erprobung und Evaluation einer bilingualen Experimentierumgebung im Fach Chemie zum Thema Carbon Capture and Storage
In Andreas Keil, Annika Hanau und Julian Dietze (Hg.): BNE in der Lehrkräftebildung. Erkenntnisse aus Forschung und Praxis., Editor, BNE in der Lehrkräftebildung - Erkenntnisse aus Forschung und Praxis
Seite 327-344
Herausgeber: Waxmann
2025
327-344ISBN: 978-3-8188-0035-2
5429.
[german] Zeller, Diana; Bohrmann-Linde, Claudia; Mack, Nils; Schrader, Claudia
VR-Lernsettings zum Thema Verbrennungsreaktionen. Ein interdisziplinäres Lehrprojekt zur Produktion von VR-Räumen durch Lehramtsstudierende
In Johannes Huwer, Timm Wilke, Amitabh Banerji, Editor, Band Progress in Digitalisation in Chemistry Education 2024 Digitales Lehren und Lernen an Hochschule und Schule im Fach Chemie
Seite 79-84
Herausgeber: Waxmann Verlag, Münster New York
2025
79-84ISBN: ISBN 978-3-8188-0042-0
5428.
Elghazi, Bouchra; Jacob, Birgit; Zwart, Hans
Well-posedness of a class of infinite-dimensional port-Hamiltonian systems with boundary control and observation
Januar 20255427.
Testa, Filippo
Well-Posedness of the Hodge Wave Equation on a Compact Manifold
2025- 2024
5426.
Jessewitsch, Till; Saou, Naima; Steinlein, Lena; Bensberg, Kathrin; Kirsch, S. F.; Delaittre, Guillaume
Oleanolic Acid-Derived High-Glass-Transition-Temperature Methacrylic Polymers
Sustainable Chemistry & Engineering, 12 :18499-18507
Dezember 2024
Herausgeber: ACS
ISSN: 2168-04855425.
Sinani, Mario; Palacios, Rafael; Wynn, Andrew
Capturing & Bounding Nonlinear Modal Energy Transfer for Geometrically Exact Beams using Semi-Definite Programming
EEE 63rd Conference on Decision and Control (CDC), 16-19 December
Dezember 20245424.
Xu, Zhuo; Tucsnak, Marius
LQR control for a system describing the interaction between a floating solid and the surrounding fluid
Mathematical Control and Related Fields, 14(4) :1477-1500
Dezember 20245423.
Klass, Friedemann; Gabbana, Alessandro; Bartel, Andreas
Perfectly Matched Layers and Characteristic Boundaries in Lattice Boltzmann: Accuracy vs Cost
AIAA Journal
Dezember 20245422.
Wissdorf, Walter; Thinius, Marco; Benter, Thorsten
Simulation of Space Charge Effects in Fourier Transform Quadrupole Ion Traps (FT-QITs)
Journal of the American Society for Mass Spectrometry, 35 (12) :2969—2983
Dezember 2024
ISSN: 1044-0305, 1879-11235421.
Liu, Qian
Small-signal synchronization stability of sequence-decomposed grid-forming IBRs
Dezember 20245420.
Bohrmann-Linde, Claudia; Kiesling, Elisabeth; Brunnert, Rainer; Strippel, C.; Landau, R.; Geller, Heidrun
Bilingual Chemistry
In Claudia Bohrmann-Linde, Rainer Brunnert, Elisabeth Kiesling, Editor, Band 1
Herausgeber: Bergische Universität Wuppertal
November 20245419.
Aydonat, Simay; Campagna, Davide; Kumar, Sourabh; Storch, Sonja; Neudecker, Tim; Göstl, Robert
Accelerated Mechanochemical Bond Scission and Stabilization against Heat and Light in Carbamoyloxime Mechanophores
Journal of the American Chemical Society, 146 (46) :32117-32123
November 2024
ISSN: 0002-7863
