Multirate
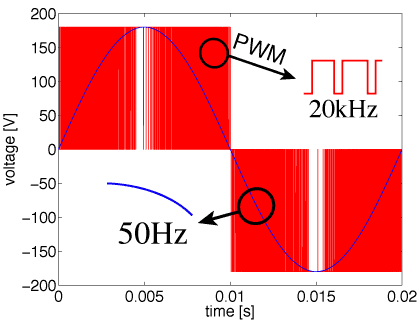
Highly integrated electric cicuits show a phenomenon called latency. That is, a processed signal causes activity only in a small subset of the whole circuit (imagine a central processing unit), whereas the other part of the system behaves almost constant over some time - is latent. Such an electric system can be described as coupled system, where the waveforms show different time scales, also refered to as multirate.
More generally, any coupled problem formulation due to coupled physical effects, may cause a multirate problem: image the simulation of car driving on the road, there you need a model for the wheel, the chassis, the dampers, the road,... (cf. co-simulation). Again each system is covered by their own time constant, which might vary over several orders of magnitude comparing different subsystems.
Classical methods cannot exploit this multirate potential, but resolve everything on the finest scale. This causes an over sampling of the latent components. In constrast, Co-simulation or especially dedicated multirate methods are designed to use the inherent step size to resolve the time-domain behaviour of each subystem with the required accuracy. This requires a time-stepping for each.
Group members working in that field
- Andreas Bartel
- Michael Günther
Former and ongoing Projects
Cooperations
- Herbert de Gersem, K.U. Leuven, Belgium
- Jan ter Maten, TU Eindhoven and NXP, the Netherlands
Publications
- 2019
3992.
Ankirchner, Stefan; Kruse, Thomas; Urusov, Mikhail
Wasserstein convergence rates for random bit approximations of continuous Markov processes
Journal of Mathematical Analysis and Applications, 493 (2) :124543
2019
Herausgeber: Academic Press3991.
Jacob, Birgit; Wegner, Sven-Ake
Well-posedness of a class of hyperbolic partial differential equations on the semi-axis
J. Evol. Equ., 19 (4) :1111--1147
20193990.
Jacob, Birgit; Kaiser, Julia T.
Well-posedness of systems of 1-{D} hyperbolic partial differential equations
J. Evol. Equ., 19 (1) :91--109
20193989.
Jacob, Birgit; Kaiser, Julia T.
Well-posedness of systems of 1-D hyperbolic partial differential equations
J. Evol. Equ., 19 (1) :91--109
20193988.
Ehrhardt, Matthias
Wide-angle mode parabolic equation with transparent boundary conditions and its applications in shallow water acoustics
2019 Days on Diffraction (DD), Seite 221–225
IEEE
Herausgeber: IEEE
20193987.
Ehrhardt, Matthias
Wide-angle mode parabolic equation with transparent boundary conditions and its applications in shallow water acoustics
2019 Days on Diffraction (DD), Seite 221--225
IEEE
20193986.
Ehrhardt, Matthias
Wide-angle mode parabolic equation with transparent boundary conditions and its applications in shallow water acoustics
2019 Days on Diffraction (DD), Seite 221–225
IEEE
Herausgeber: IEEE
20193985.
Cuny, Christophe; Eisner, Tanja; Farkas, Bálint
Wiener's lemma along primes and other subsequences
Advances in Mathematics, 347 :340 - 383
20193984.
Jacob, Birgit; Morris, Kirsten A.; Zwart, Hans
Zero dynamics for networks of waves
Automatica J. IFAC, 103 :310--321
2019- 2018
3983.
Sharma, M. K.; Göstl, Robert; Frijns, A. J. H.; Wieringa, F. P.; Kooman, J. P.; Sijbesma, R. P.; Smeulders, D. M. J.
A Fluorescent Micro-Optofluidic Sensor for In-Line Ion Selective Electrolyte Monitoring
IEEE Sensors Journal, 18 (10) :3946--3951
Mai 2018
ISSN: 1530-437X3982.
[1,2]-Migration Reactions Catalyzed by Gold Complexes and their Applications in Total Synthesis
Israel Journal of Chemistry, 58 (5) :596–607
2018
ISSN: 1869-58683981.
Jacob, Birgit; Partington, Jonathan R.; Pott, Sandra; Wynn, Andrew
{\(\beta\)}-admissibility of observation operators for hypercontractive semigroups
J. Evol. Equ., 18 (1) :153--170
20183980.
Jacob, Birgit; Partington, Jonathan R.; Pott, Sandra; Wynn, Andrew
β-admissibility of observation operators for hypercontractive semigroups
J. Evol. Equ., 18 (1) :153--170
20183979.
Daners, Daniel; Glück, Jochen
A criterion for the uniform eventual positivity of operator semigroups
Integral Equations Operator Theory, 90 (4) :Paper No. 46, 19
20183978.
Farkas, Bálint; Nagy, Béla; Révész, Szilárd Gy.
A minimax problem for sums of translates on the torus
Transactions of the London Mathematical Society, 5 (1) :1-46
20183977.
Kossaczky, Igor; Ehrhardt, Matthias; Günther, Michael
A new convergent explicit tree-grid method for HJB equations in one space dimension
Numerical Mathematics: Theory, Methods and Applications, 11 (1) :1–29
2018
Herausgeber: Global Science Press3976.
Ehrhardt, Matthias; Günther, Michael
A new convergent explicit Tree-Grid method for HJB equations in one space dimension
Preprint, 17 (06)
20183975.
Kossaczky, Igor; Ehrhardt, Matthias; Günther, Michael
A new convergent explicit tree-grid method for HJB equations in one space dimension
Numerical Mathematics: Theory, Methods and Applications, 11 (1) :1–29
2018
Herausgeber: Global Science Press3974.
Kossaczky, Igor; Ehrhardt, Matthias; Günther, Michael
A new convergent explicit tree-grid method for HJB equations in one space dimension
Numerical Mathematics: Theory, Methods and Applications, 11 (1) :1–29
2018
Herausgeber: Global Science Press3973.
Heilmann, Margareta; Raşa, Ioan
A nice representation for a link between Baskakov-and Szász–Mirakjan–Durrmeyer operators and their kantorovich variants
Results in Mathematics, 74 (1) :9
20183972.
Glück, Jochen
A note on lattice ordered $C^*$-algebras and Perron-Frobenius theory
Math. Nachr., 291 (11-12) :1727--1732
20183971.
Bartel, Andreas; Ehrhardt, Matthias
A numerical tool for the study of the hydrodynamic recovery of the lattice Boltzmann Method
Computers & Fluids, 172 :241–250
2018
Herausgeber: Pergamon3970.
Bartel, Andreas; Ehrhardt, Matthias
A numerical tool for the study of the hydrodynamic recovery of the Lattice Boltzmann Method
Computers & Fluids, 172 :241--250
2018
Herausgeber: Pergamon3969.
Bartel, Andreas; Ehrhardt, Matthias
A numerical tool for the study of the hydrodynamic recovery of the lattice Boltzmann Method
Computers & Fluids, 172 :241–250
2018
Herausgeber: Pergamon3968.
Harbrecht, Helmut; Zaspel, Peter
A scalable H-matrix approach for the solution of boundary integral equations on multi-GPU clusters
2018
