Dynamic Iteration Schemes
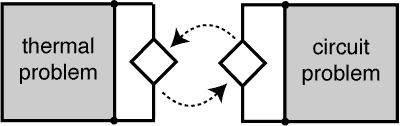
Dynamic iteration via source coupling
Standard time-integration methods solve transient problems all at once. This may become very inefficient or impossible for large systems of equations. Imaging that such large systems often stem from a coupled problem formulation, where different physical phenomena interact and need to be coupled in order to produce a precise mathematical model.
E.g. highly integrated electric circuits (as in memory chips or CPUs) produce heat, which effects in turn their behavior as electrical system; thus one needs to couple electric and thermal subproblem descriptions. On the one hand, this creates multiple time scales due to different physical phenomena, which demands an efficient treatment, see multirate. On the other hand, in a professional environment one usually has dedicated solvers for the subproblems, which need to be used, and an overall problem formulation is not feasible for any of the involved tools.
For those partitioned problems a dynamic iteration method becomes beneficial or even the sole way-out: it keeps the subproblems separate, solves subproblems sequentially (or in parallel) and iterates until convergence (fixed-point interation). Thus the subproblem's structure can be exploited in the respective integration.
To guarantee or to speed up convergence the time interval of interest is split into a series of windows. Then the time-integration of the windows is applied sequentially and in each window the subproblems are solved iteratively by your favoured method.
Group members working on that field
- Andreas Bartel
- Michael Günther
Former and ongoing Projects
Cooperation
- Herbert De Gersem, Katholieke Universiteit Leuven
Publications
- 2019
3992.
Ankirchner, Stefan; Kruse, Thomas; Urusov, Mikhail
Wasserstein convergence rates for random bit approximations of continuous Markov processes
Journal of Mathematical Analysis and Applications, 493 (2) :124543
2019
Herausgeber: Academic Press3991.
Jacob, Birgit; Wegner, Sven-Ake
Well-posedness of a class of hyperbolic partial differential equations on the semi-axis
J. Evol. Equ., 19 (4) :1111--1147
20193990.
Jacob, Birgit; Kaiser, Julia T.
Well-posedness of systems of 1-{D} hyperbolic partial differential equations
J. Evol. Equ., 19 (1) :91--109
20193989.
Jacob, Birgit; Kaiser, Julia T.
Well-posedness of systems of 1-D hyperbolic partial differential equations
J. Evol. Equ., 19 (1) :91--109
20193988.
Ehrhardt, Matthias
Wide-angle mode parabolic equation with transparent boundary conditions and its applications in shallow water acoustics
2019 Days on Diffraction (DD), Seite 221–225
IEEE
Herausgeber: IEEE
20193987.
Ehrhardt, Matthias
Wide-angle mode parabolic equation with transparent boundary conditions and its applications in shallow water acoustics
2019 Days on Diffraction (DD), Seite 221--225
IEEE
20193986.
Ehrhardt, Matthias
Wide-angle mode parabolic equation with transparent boundary conditions and its applications in shallow water acoustics
2019 Days on Diffraction (DD), Seite 221–225
IEEE
Herausgeber: IEEE
20193985.
Cuny, Christophe; Eisner, Tanja; Farkas, Bálint
Wiener's lemma along primes and other subsequences
Advances in Mathematics, 347 :340 - 383
20193984.
Jacob, Birgit; Morris, Kirsten A.; Zwart, Hans
Zero dynamics for networks of waves
Automatica J. IFAC, 103 :310--321
2019- 2018
3983.
Sharma, M. K.; Göstl, Robert; Frijns, A. J. H.; Wieringa, F. P.; Kooman, J. P.; Sijbesma, R. P.; Smeulders, D. M. J.
A Fluorescent Micro-Optofluidic Sensor for In-Line Ion Selective Electrolyte Monitoring
IEEE Sensors Journal, 18 (10) :3946--3951
Mai 2018
ISSN: 1530-437X3982.
[1,2]-Migration Reactions Catalyzed by Gold Complexes and their Applications in Total Synthesis
Israel Journal of Chemistry, 58 (5) :596–607
2018
ISSN: 1869-58683981.
Jacob, Birgit; Partington, Jonathan R.; Pott, Sandra; Wynn, Andrew
{\(\beta\)}-admissibility of observation operators for hypercontractive semigroups
J. Evol. Equ., 18 (1) :153--170
20183980.
Jacob, Birgit; Partington, Jonathan R.; Pott, Sandra; Wynn, Andrew
β-admissibility of observation operators for hypercontractive semigroups
J. Evol. Equ., 18 (1) :153--170
20183979.
Daners, Daniel; Glück, Jochen
A criterion for the uniform eventual positivity of operator semigroups
Integral Equations Operator Theory, 90 (4) :Paper No. 46, 19
20183978.
Farkas, Bálint; Nagy, Béla; Révész, Szilárd Gy.
A minimax problem for sums of translates on the torus
Transactions of the London Mathematical Society, 5 (1) :1-46
20183977.
Kossaczky, Igor; Ehrhardt, Matthias; Günther, Michael
A new convergent explicit tree-grid method for HJB equations in one space dimension
Numerical Mathematics: Theory, Methods and Applications, 11 (1) :1–29
2018
Herausgeber: Global Science Press3976.
Ehrhardt, Matthias; Günther, Michael
A new convergent explicit Tree-Grid method for HJB equations in one space dimension
Preprint, 17 (06)
20183975.
Kossaczky, Igor; Ehrhardt, Matthias; Günther, Michael
A new convergent explicit tree-grid method for HJB equations in one space dimension
Numerical Mathematics: Theory, Methods and Applications, 11 (1) :1–29
2018
Herausgeber: Global Science Press3974.
Kossaczky, Igor; Ehrhardt, Matthias; Günther, Michael
A new convergent explicit tree-grid method for HJB equations in one space dimension
Numerical Mathematics: Theory, Methods and Applications, 11 (1) :1–29
2018
Herausgeber: Global Science Press3973.
Heilmann, Margareta; Raşa, Ioan
A nice representation for a link between Baskakov-and Szász–Mirakjan–Durrmeyer operators and their kantorovich variants
Results in Mathematics, 74 (1) :9
20183972.
Glück, Jochen
A note on lattice ordered $C^*$-algebras and Perron-Frobenius theory
Math. Nachr., 291 (11-12) :1727--1732
20183971.
Bartel, Andreas; Ehrhardt, Matthias
A numerical tool for the study of the hydrodynamic recovery of the lattice Boltzmann Method
Computers & Fluids, 172 :241–250
2018
Herausgeber: Pergamon3970.
Bartel, Andreas; Ehrhardt, Matthias
A numerical tool for the study of the hydrodynamic recovery of the Lattice Boltzmann Method
Computers & Fluids, 172 :241--250
2018
Herausgeber: Pergamon3969.
Bartel, Andreas; Ehrhardt, Matthias
A numerical tool for the study of the hydrodynamic recovery of the lattice Boltzmann Method
Computers & Fluids, 172 :241–250
2018
Herausgeber: Pergamon3968.
Harbrecht, Helmut; Zaspel, Peter
A scalable H-matrix approach for the solution of boundary integral equations on multi-GPU clusters
2018
