Dynamic Iteration Schemes
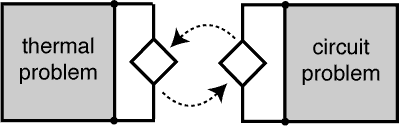
Dynamic iteration via source coupling
Standard time-integration methods solve transient problems all at once. This may become very inefficient or impossible for large systems of equations. Imaging that such large systems often stem from a coupled problem formulation, where different physical phenomena interact and need to be coupled in order to produce a precise mathematical model.
E.g. highly integrated electric circuits (as in memory chips or CPUs) produce heat, which effects in turn their behavior as electrical system; thus one needs to couple electric and thermal subproblem descriptions. On the one hand, this creates multiple time scales due to different physical phenomena, which demands an efficient treatment, see multirate. On the other hand, in a professional environment one usually has dedicated solvers for the subproblems, which need to be used, and an overall problem formulation is not feasible for any of the involved tools.
For those partitioned problems a dynamic iteration method becomes beneficial or even the sole way-out: it keeps the subproblems separate, solves subproblems sequentially (or in parallel) and iterates until convergence (fixed-point interation). Thus the subproblem's structure can be exploited in the respective integration.
To guarantee or to speed up convergence the time interval of interest is split into a series of windows. Then the time-integration of the windows is applied sequentially and in each window the subproblems are solved iteratively by your favoured method.
Group members working on that field
- Andreas Bartel
- Michael Günther
Former and ongoing Projects
Cooperation
- Herbert De Gersem, Katholieke Universiteit Leuven
Publications
- 1996
618.
Kozin, Igor N.; Jensen, Per; Polanz, Oliver; Klee, Stefan; Poteau, Laurent; Demaison, Jean
The Rotational Spectrum of H2Te
Journal of Molecular Spectroscopy, 180 (2) :402-413
1996
Herausgeber: Academic Press617.
Bunker, Philip R.; Jensen, Per; Yamaguchi, Yukio; Schaefer III, Henry F.
The Rovibrational Energy Levels of Quasilinear c\verb=~= \(^{1}\)A\(_{1}\) Methylene
Journal of Molecular Spectroscopy, 179 (2) :263-268
1996
Herausgeber: Academic Press616.
Bunker, Philip R.; Jensen, Per; Yamaguchi, Yukio; Schaefer III, Henry F.
The Rovibrational Energy Levels of Quasilinear c\verb=~= \(^{1}\)A\(_{1}\) Methylene
Journal of Molecular Spectroscopy, 179 (2) :263-268
1996
Herausgeber: Academic Press615.
Bunker, Philip R.; Jensen, Per; Yamaguchi, Yukio; Schaefer III, Henry F.
The Rovibrational Energy Levels of Quasilinear c~ 1A1 Methylene
Journal of Molecular Spectroscopy, 179 (2) :263-268
1996
Herausgeber: Academic Press614.
Arste, J.; Klamroth, Kathrin; Mengersen, Ingrid
Three color Ramsey numbers for small graphs
Utilitas Mathematica, 49 :85--96
1996613.
[german] Tausch, Michael W.
Ungleiche Gleichgewichte
{CHEMKON}, 3 (3) :123--127
1996
Herausgeber: Wiley- 1995
612.
Mengel, Markus; Jensen, Per
A Theoretical Study of the Stark Effect in Triatomic Molecules: Application to H\(_{2}\)O
Journal of Molecular Spectroscopy, 169 (1) :73-91
1995
Herausgeber: Academic Press611.
Mengel, Markus; Jensen, Per
A Theoretical Study of the Stark Effect in Triatomic Molecules: Application to H\(_{2}\)O
Journal of Molecular Spectroscopy, 169 (1) :73-91
1995
Herausgeber: Academic Press610.
Mengel, Markus; Jensen, Per
A Theoretical Study of the Stark Effect in Triatomic Molecules: Application to H2O
Journal of Molecular Spectroscopy, 169 (1) :73-91
1995
Herausgeber: Academic Press609.
Jensen, Per; Brumm, Martin; Kraemer, Wolfgang P.; Bunker, Philip R.
A Treatment of the Renner Effect Using the MORBID Hamiltonian
Journal of Molecular Spectroscopy, 171 (1) :31-57
1995
Herausgeber: Academic Press608.
Jensen, Per; Brumm, Martin; Kraemer, Wolfgang P.; Bunker, Philip R.
A Treatment of the Renner Effect Using the MORBID Hamiltonian
Journal of Molecular Spectroscopy, 171 (1) :31-57
1995
Herausgeber: Academic Press607.
Jensen, Per; Brumm, Martin; Kraemer, Wolfgang P.; Bunker, Philip R.
A Treatment of the Renner Effect Using the MORBID Hamiltonian
Journal of Molecular Spectroscopy, 171 (1) :31-57
1995
Herausgeber: Academic Press606.
Jensen, Per; Brumm, Martin; Kraemer, Wolfgang P.; Bunker, Philip R.
An ab Initio Calculation of the Rovibronic Energies of the CH\(_{2}\)\(^{+}\) Molecule
Journal of Molecular Spectroscopy, 172 (1) :194-204
1995
Herausgeber: Academic Press605.
Jensen, Per; Brumm, Martin; Kraemer, Wolfgang P.; Bunker, Philip R.
An ab Initio Calculation of the Rovibronic Energies of the CH\(_{2}\)\(^{+}\) Molecule
Journal of Molecular Spectroscopy, 172 (1) :194-204
1995
Herausgeber: Academic Press604.
Jensen, Per; Brumm, Martin; Kraemer, Wolfgang P.; Bunker, Philip R.
An ab Initio Calculation of the Rovibronic Energies of the CH2+ Molecule
Journal of Molecular Spectroscopy, 172 (1) :194-204
1995
Herausgeber: Academic Press603.
Gerstberger, R.; Günther, M.
Charge-oriented extrapolation methods in digital circuit simulation
Applied Numerical Mathematics, 18 (1) :115–125
1995
Herausgeber: Elsevier602.
Gerstberger, Robert; Günther, Michael
Charge-oriented extrapolation methods in digital circuit simulation
Applied numerical mathematics, 18 (1-3) :115--125
1995
Herausgeber: North-Holland601.
Flaud, Jean-Marie; Camy-Peyret, C.; B{ü}rger, H.; Jensen, Per; Kozin, Igor N.
Experimental evidence for the formation of fourfold rovibrational energy clusters in the \(\nu\)\(_{1}\)/\(\nu\)\(_{3}\) vibrational states of H\(_{2}\)\(^{80}\)Se
Journal of Molecular Spectroscopy, 172 (1) :126-134
1995
Herausgeber: Academic Press600.
Flaud, Jean-Marie; Camy-Peyret, C.; B{ü}rger, H.; Jensen, Per; Kozin, Igor N.
Experimental evidence for the formation of fourfold rovibrational energy clusters in the \(\nu\)\(_{1}\)/\(\nu\)\(_{3}\) vibrational states of H\(_{2}\)\(^{80}\)Se
Journal of Molecular Spectroscopy, 172 (1) :126-134
1995
Herausgeber: Academic Press599.
Flaud, Jean-Marie; Camy-Peyret, C.; Bürger, H.; Jensen, Per; Kozin, Igor N.
Experimental evidence for the formation of fourfold rovibrational energy clusters in the ν1/ν3 vibrational states of H280Se
Journal of Molecular Spectroscopy, 172 (1) :126-134
1995
Herausgeber: Academic Press598.
Heilmann, Margareta
Explicit Voronovskaja-type results for linear combinations of BDT-operators
Approximation Theory and its Applications, 11 (1) :54-61
1995597.
Ehrhardt, M.
Finite Differenzenverfahren für hyperbolische Systeme mit absorbierenden Randbedingungen
Technische Universität Berlin
1995596.
Jensen, Per; Li, Yan; Hirsch, Gerhard; Buenker, Robert J.; Lee, Timothy J.; Kozin, Igor N.
Fourfold clusters of rovibrational energies in H\(_{2}\)Te studied with an ab initio potential energy function
Chemical Physics, 190 (2-3) :179-189
1995595.
Jensen, Per; Li, Yan; Hirsch, Gerhard; Buenker, Robert J.; Lee, Timothy J.; Kozin, Igor N.
Fourfold clusters of rovibrational energies in H\(_{2}\)Te studied with an ab initio potential energy function
Chemical Physics, 190 (2-3) :179-189
1995594.
Jensen, Per; Li, Yan; Hirsch, Gerhard; Buenker, Robert J.; Lee, Timothy J.; Kozin, Igor N.
Fourfold clusters of rovibrational energies in H2Te studied with an ab initio potential energy function
Chemical Physics, 190 (2-3) :179-189
1995
