Computational Magnetics
Many electro-technical devices such as e.g. printed circuit boards, electrical drives and antenna systems can be simulated on the basis of electrical circuits. However, the increasing frequencies and the decreasing size force designers to account for wave propagation effects, eddy-current effects, ferromagnetic saturation and hysteresis. For wave propagation effects and eddy-current effects, the results of stand-alone field simulation can be represented by an order-reduced equivalent model, which is then inserted in the overall circuit model. The representation of field-dependent nonlinearities and hysteresis effects, however, is not straightforward.
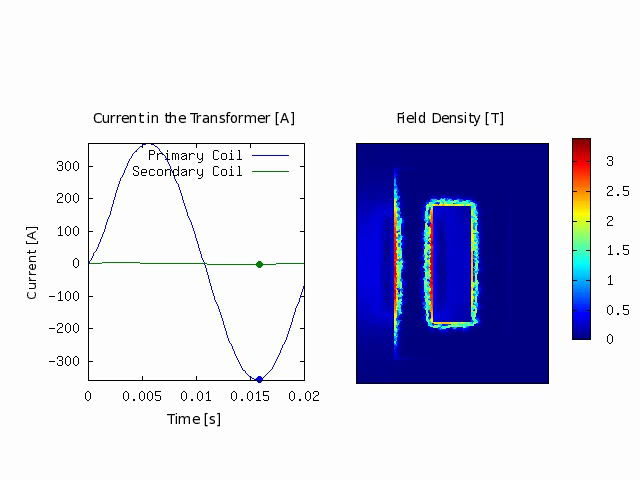
2D Simulation of a Transformer
The coupled field and circuit simulation becomes troublesome when a large number of time steps is required. This occurs when e.g. simulating an electrical drive where the machine requires 10 periods of 50 Hz to reach nominal speed whereas the switching of the Insulated Gate Bipolar Transistors in the frequency converter switches at 20 kHz, necessitating a time steps in the order of a microsecond to be used in the simulation. Since the field model consists typically of a few million degrees of freedom, all those unknowns have to be solved in every time step. Fortunately, the relevant time constants in electrical-energy converter are in the range 50 Hz. Hence the field model does not have to be time-stepped at the same rate as the circuit model, in which fast switches are present. The use of adaptive multirate time-integration schemes can reduce the numerical complexity of the problem substantially.
Research Questions
- Efficiency of the time-integration for field devices in pulsed circuits (multirate, dynamic iteration)
- DAE-index of the coupled system
- Existence and Uniqueness of the solution
Cooperation
- Herbert De Gersem, Katholieke Universiteit Leuven
- Markus Clemens, Bergische Universität Wuppertal
- Sascha Baumanns, Universität zu Köln
Former and ongoing projects
Publications
- 1983
67.
Jensen, Per
The nonrigid bender Hamiltonian for calculating the rotation-vibration energy levels of a triatomic molecule
Computer Physics Reports, 1 (1) :1-55
198366.
Jensen, Per
The nonrigid bender Hamiltonian for calculating the rotation-vibration energy levels of a triatomic molecule
Computer Physics Reports, 1 (1) :1-55
198365.
Holstein, K. J.; Fink, Ewald H.; Zabel, Friedhelm
The ν3 vibration of electronically excited HO2(A2A')
Journal of Molecular Spectroscopy, 99 (1) :231-234
1983- 1982
64.
Winter, R.; Barnes, Ian; Fink, Ewald H.; Wildt, J{ü}rgen; Zabel, Friedhelm
b\(^{1}\)\(\Sigma\)\(^{+}\) and a\(^{1}\)\(\Delta\) emissions from group VI-VI diatomic molecules b0\(_{g}\)\(^{+}\) → X\(^{2}\)1\(_{g}\) emissions of Se\(_{2}\) and Te\(_{2}\)
Chemical Physics Letters, 86 (2) :118-122
198263.
Winter, R.; Barnes, Ian; Fink, Ewald H.; Wildt, J{ü}rgen; Zabel, Friedhelm
b\(^{1}\)\(\Sigma\)\(^{+}\) and a\(^{1}\)\(\Delta\) emissions from group VI-VI diatomic molecules b0\(_{g}\)\(^{+}\) → X\(^{2}\)1\(_{g}\) emissions of Se\(_{2}\) and Te\(_{2}\)
Chemical Physics Letters, 86 (2) :118-122
198262.
Winter, R.; Barnes, Ian; Fink, Ewald H.; Wildt, J{ü}rgen; Zabel, Friedhelm
b\(^{1}\)\(\Sigma\)\(^{+}\) and a\(^{1}\)\(\Delta\) emissions from group VI-VI diatomic molecules: b0\(^{+}\) → X\(_{1}\)0\(^{+}\), X\(_{2}\)1 emissions of TeO and TeS
Journal of Molecular Structure, 80 :75-82
198261.
Winter, R.; Barnes, Ian; Fink, Ewald H.; Wildt, J{ü}rgen; Zabel, Friedhelm
b\(^{1}\)\(\Sigma\)\(^{+}\) and a\(^{1}\)\(\Delta\) emissions from group VI-VI diatomic molecules: b0\(^{+}\) → X\(_{1}\)0\(^{+}\), X\(_{2}\)1 emissions of TeO and TeS
Journal of Molecular Structure, 80 :75-82
198260.
Kruse, H.; Winter, R.; Fink, Ewald H.; Wildt, J{ü}rgen; Zabel, Friedhelm
b\(^{1}\)\(\Sigma\)\(^{+}\) emissions from group V-VII diatomic molecules: b0\(^{+}\) → X\(_{1}\)0\(^{+}\), X\(_{2}\)0\(^{+}\) emissions of SbBr
Chemical Physics Letters, 93 (5) :475-479
198259.
Kruse, H.; Winter, R.; Fink, Ewald H.; Wildt, J{ü}rgen; Zabel, Friedhelm
b\(^{1}\)\(\Sigma\)\(^{+}\) emissions from group V-VII diatomic molecules: b0\(^{+}\) → X\(_{1}\)0\(^{+}\), X\(_{2}\)0\(^{+}\) emissions of SbBr
Chemical Physics Letters, 93 (5) :475-479
198258.
Winter, R.; Barnes, Ian; Fink, Ewald H.; Wildt, Jürgen; Zabel, Friedhelm
b1Σ+ and a1Δ emissions from group VI-VI diatomic molecules b0g+ → X21g emissions of Se2 and Te2
Chemical Physics Letters, 86 (2) :118-122
198257.
Winter, R.; Barnes, Ian; Fink, Ewald H.; Wildt, Jürgen; Zabel, Friedhelm
b1Σ+ and a1Δ emissions from group VI-VI diatomic molecules: b0+ → X10+, X21 emissions of TeO and TeS
Journal of Molecular Structure, 80 :75-82
198256.
Kruse, H.; Winter, R.; Fink, Ewald H.; Wildt, Jürgen; Zabel, Friedhelm
b1Σ+ emissions from group V-VII diatomic molecules: b0+ → X10+, X20+ emissions of SbBr
Chemical Physics Letters, 93 (5) :475-479
198255.
Tausch, Michael W.
Modelle im Chemieunterricht
Der mathematische und naturwissenschaftliche Unterricht (MNU), 35 :226
198254.
Becker, Karl Heinz; Horie, O.; Schmidt, V. H.; Wiesen, Peter
Spectroscopic identification of C\(_{2}\)O radicals in the C\(_{3}\)O\(_{2}\) + O flame system by laser-induced fluorescence
Chemical Physics Letters, 90 (1) :64-68
198253.
Becker, Karl Heinz; Horie, O.; Schmidt, V. H.; Wiesen, Peter
Spectroscopic identification of C\(_{2}\)O radicals in the C\(_{3}\)O\(_{2}\) + O flame system by laser-induced fluorescence
Chemical Physics Letters, 90 (1) :64-68
198252.
Becker, Karl Heinz; Horie, O.; Schmidt, V. H.; Wiesen, Peter
Spectroscopic identification of C2O radicals in the C3O2 + O flame system by laser-induced fluorescence
Chemical Physics Letters, 90 (1) :64-68
198251.
Jensen, Per; Brodersen, Svend
The \(\nu\)\(_{5}\) Raman band of CH\(_{3}\)CD\(_{3}\)
Journal of Raman Spectroscopy, 12 (3) :295-299
198250.
Jensen, Per; Brodersen, Svend
The \(\nu\)\(_{5}\) Raman band of CH\(_{3}\)CD\(_{3}\)
Journal of Raman Spectroscopy, 12 (3) :295-299
198249.
Jensen, Per; Bunker, Philip R.; Hoy, A. R.
The equilibrium geometry, potential function, and rotation?vibration energies of CH\(_{2}\) in the X\verb=~=\(^{3}\)B\(_{1}\) ground state
The Journal of Chemical Physics, 77 (11) :5370-5374
198248.
Jensen, Per; Bunker, Philip R.; Hoy, A. R.
The equilibrium geometry, potential function, and rotation?vibration energies of CH\(_{2}\) in the X\verb=~=\(^{3}\)B\(_{1}\) ground state
The Journal of Chemical Physics, 77 (11) :5370-5374
198247.
Jensen, Per; Bunker, Philip R.; Hoy, A. R.
The equilibrium geometry, potential function, and rotation?vibration energies of CH2 in the X~3B1 ground state
The Journal of Chemical Physics, 77 (11) :5370-5374
198246.
Jensen, Per; Bunker, Philip R.
The geometry and the inversion potential function of formaldehyde in the and electronic states
Journal of Molecular Spectroscopy, 94 (1) :114-125
198245.
Jensen, Per; Bunker, Philip R.
The geometry and the inversion potential function of formaldehyde in the and electronic states
Journal of Molecular Spectroscopy, 94 (1) :114-125
198244.
Jensen, Per; Bunker, Philip R.
The geometry and the inversion potential function of formaldehyde in the and electronic states
Journal of Molecular Spectroscopy, 94 (1) :114-125
198243.
Jensen, Per; Bunker, Philip R.
The geometry and the out-of-plane bending potential function of thioformaldehyde in the A\verb=~=\(^{1}\)A\(_{2}\) and a\verb=~=\(^{3}\)A\(_{2}\) electronic states
Journal of Molecular Spectroscopy, 95 (1) :92-100
1982
