Coupled DAE Problems
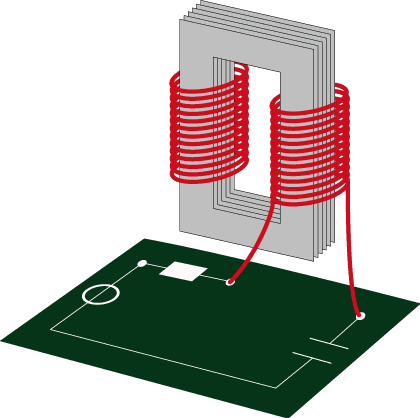
A circuit (DAE model) coupled to a magnetostatic field device (PDE model)
Coupled Problems of differential-algebraic equations (DAEs) arise typically from either multiphysical modeling (e.g. in circuit simulation with heating) or from refined modeling, where crucial parts of the original problem are replaced by a better, but computational more expensive model (e.g. circuits refined by field models). Furthermore splitting methods may turn a monolithic DAE problem into coupled subproblems, e.g. because of different time scales (multirate). In any case the DAEs arise from network approaches or space-discretization of PDAEs (Partial Differential Algebraic Equations).
Often the coupled equations have quite different properties, i.e., symmetries, definiteness or time scales. Thus the coupled system must be analyzed (e.g. the index) and tailored methods have to be developed (e.g. dynamic iteration).
Details
Publications
- 2024
5342.
Fan, Jilin; Zhang, Kuan; Xuan, Mingjun; Gao, Xiang; Vinokur, Rostislav; Göstl, Robert; Zheng, Lifei; Herrmann, Andreas
High-Intensity Focused Ultrasound-Induced Disulfide Mechanophore Activation in Polymeric Nanostructures for Molecule Release
CCS Chemistry, 6 (8) :1895-1907
August 20245341.
Tapera, Michael; Borghi, Federica; Mayer-Figge, Jan Lukas; Mittendorf, Fabia; Celik, I. E.; Gómez-Suárez, Adrián; Kirsch, S. F.
A Formal Synthesis of (+)-Hannokinol Using a Chiral Horner–Wittig Reagent
Molecules, 29 :3710
07 2024
Publisher: MDPI
ISSN: 1420-30495340.
Alcalde, Albert; Fantuzzi, Giovanni; Zuazua, Enrique
Clustering in pure-attention hardmax transformers and its role in sentiment analysis
06 20245339.
Ballaschk, Frederic; Bensberg, Kathrin; Crone, Benedikt; Kirsch, S. F.; Menz, Helge
Synthesis of the monomeric counterpart of Marinomycin A and B
Organic & Biomolecular Chemistry, 2024
06 2024
Publisher: RSC5338.
Aydonat, Simay; Hergesell, Adrian H.; Seitzinger, Claire L.; Lennarz, Regina; Chang, George; Sievers, Carsten; Meisner, Jan; Vollmer, Ina; Göstl, Robert
Leveraging mechanochemistry for sustainable polymer degradation
Polymer Journal, 56 (4) :249-268
April 2024
ISSN: 1349-05405337.
Glück, Jochen; Mui, Jonathan
Non-positivity of the heat equation with non-local Robin boundary conditions
04 20245336.
[german] Tausch, Michael W.
Curriculare Innovation - Ein Imperativ für den Chemieunterricht
Volume Chemie professionell unterrichten
Publisher: T. Palenta
February 2024ISBN: 9783758478413
5335.
Rath, Wolfgang H.; Göstl, Robert; Herrmann, Andreas
Mechanochemical Activation of DNAzyme by Ultrasound
Advanced Science, 11 (8) :2306236
February 2024
ISSN: 2198-38445334.
Celik, I. E.; Mittendorf, Fabia; Gómez-Suárez, Adrián; Kirsch, S. F.
Formal synthesis of bastimolide A using a chiral Horner-Wittig reagent and a bifunctional aldehyde as key building blocks
Tetrahedron Chem, 9
02 2024
Publisher: Elsevier
ISSN: 2666-951X5333.
Bensberg, Kathrin; Savvidis, Athanasios; Ballaschk, Frederic; Gómez-Suárez, Adrián; Kirsch, S. F.
Oxidation of Alcohols in Continuous Flow with a SolidPhase Hypervalent Iodine Catalyst
Chemistry - A European Journal, 2024 :e202304011
02 2024
Publisher: Wiley
ISSN: 0947-65395332.
[german] Tausch, Michael W.; Schneidewind, Jacob
Mit Licht zu grünem Wasserstoff
Chemie in unserer Zeit, 58 (1)
February 20245331.
Izak-Nau, Emilia; Niggemann, Louisa P.; Göstl, Robert
Brownian Relaxation Shakes and Breaks Magnetic Iron Oxide-Polymer Nanocomposites to Release Cargo
Small, 20 (4) :2304527
January 2024
ISSN: 1613-68295330.
[english] Wiebel, Michelle; Bensberg, Kathrin; Wende, Luca; Grandrath, Rebecca; Plitzko, Kathrin; Bohrmann-Linde, Claudia; Kirsch, Stefan F.; Schebb, Nils Helge
Efficient and simple extraction protocol for triterpenic acids from apples
Journal of Chemical Education
April 2024
Publisher: American Chemical Society and Division of Chemical Education, Inc.5329.
Jessewitsch, Till; Saou, Naima; Steinlein, Lena; Bensberg, Kathrin; Kirsch, S. F.; Delaittre, Guillaume
Oleanolic Acid-Derived High-Glass-Transition-Temperature Methacrylic Polymers
Sustainable Chemistry & Engineering
December 2024
Publisher: ACS
ISSN: 2168-04855328.
Krhac, Kaja; Maschke, Bernhard; van der Schaft, Arjan
Port-Hamiltonian systems with energy and power ports
IFAC-PapersOnLine, 58(6) :280-285
May 20245327.
Kapllani, Lorenc; Teng, Long
{A backward differential deep learning-based algorithm for solving high-dimensional nonlinear backward stochastic differential equations}
20245326.
Ehrhardt, Matthias; Kozitskiy, Sergey B
A generalization of the split-step Padé method to the case of coupled acoustic modes equation in a 3D waveguide
Journal of Sound and Vibration :118304
2024
Publisher: Elsevier5325.
Petrov, Pavel S.; Ehrhardt, Matthias; Kozitskiy, Sergey B.
A generalization of the split-step Padé method to the case of coupled acoustic modes equation in a 3D waveguide
Journal of Sound and Vibration, 577 :118304
2024
Publisher: Academic Press5324.
Petrov, Pavel S.; Ehrhardt, Matthias; Kozitskiy, Sergey B.
A generalization of the split-step Padé method to the case of coupled acoustic modes equation in a 3D waveguide
Journal of Sound and Vibration, 577 :118304
2024
Publisher: Academic Press5323.
Clevenhaus, Anna; Totzeck, Claudia; Ehrhardt, Matthias
A gradient-based calibration method for the Heston model
International Journal of Computer Mathematics, 101 (9-10) :1094–1112
2024
Publisher: Taylor & Francis5322.
Clevenhaus, Anna; Totzeck, Claudia; Ehrhardt, Matthias
A gradient-based calibration method for the Heston model
International Journal of Computer Mathematics, 101 (9-10) :1094–1112
2024
Publisher: Taylor & Francis5321.
Clevenhaus, Anna; Totzeck, Claudia; Ehrhardt, Matthias
A gradient-based calibration method for the Heston model
International Journal of Computer Mathematics
20245320.
Schäfers, Kevin; Peardon, Michael; Günther, Michael
A modified Cayley transform for SU (3)
Preprint
20245319.
Schäfers, Kevin; Peardon, Michael; Günther, Michael
A modified Cayley transform for SU (3)
Preprint
20245318.
Schaefers, Kevin; Peardon, Michael
A modified Cayley transform for SU(3)
2024
