Polynomial Chaos for Uncertainty Quantification
Uncertainty quantification becomes a more and more important task in many applications. Given a physical or technical system, the impact of uncertainties in the inputs has to be determined for the outputs. Consequently, the inputs are replaced by random variables in the corresponding mathematical models. The original models may be ordinary differential equations (ODEs), differential algebraic equations (DAEs) or partial differential equations (PDEs). The random process satisfying the stochastic system has to be computed by numerical methods.
A Monte-Carlo simulation is able to resolve the stochastic model, for example. Typically, the original deterministic system has to be solved a huge number of times to achieve sufficiently accurate approximations in a Monte-Carlo simulation. Alternatively, the technique of the polynomial chaos applies an expansion of the random process via a series with orthogonal basis polynomials. A Galerkin method yields a larger coupled system of ODEs, DAEs or PDEs, respectively, whose solution represents an approximation of the random process. Now the larger coupled system has to be solved just once to obtain this approximation. In some cases, the technique of the polynomial chaos is significantly more efficient than a Monte-Carlo simulation. It follows that the type and the properties of the larger coupled system have to be analysed in each application. Corresponding numerical methods have to be adapted to the specific properties of the larger coupled system if a standard type is not given.
The approach of the polynomial chaos can be used in each application, where mathematical models based on ODEs, DAEs or PDEs appear. In particular, mechanical engineering (stochastic finite elements), electrical engineering, chemical reaction kinetics and computational fluid dynamics represent active fields of research concerning uncertainty quantification via polynomial chaos. Furthermore, applications like computational finance or radio frequency circuits have been considered previously.
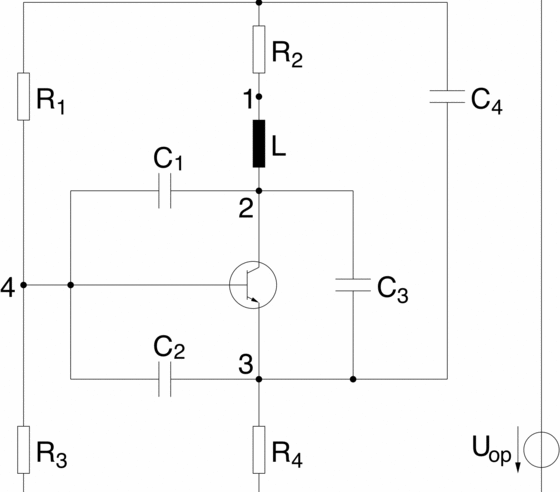
Electric circuit of Colpitts oscillator
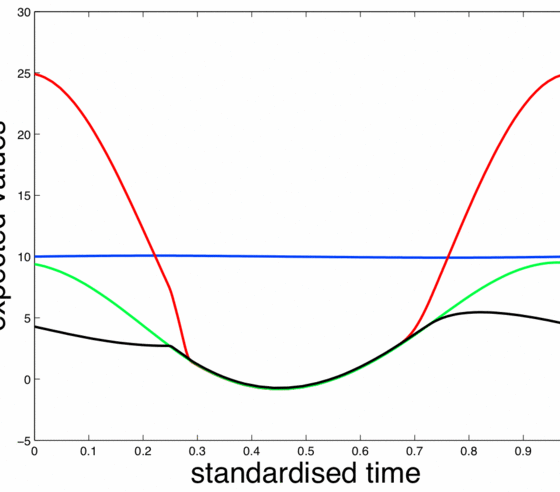
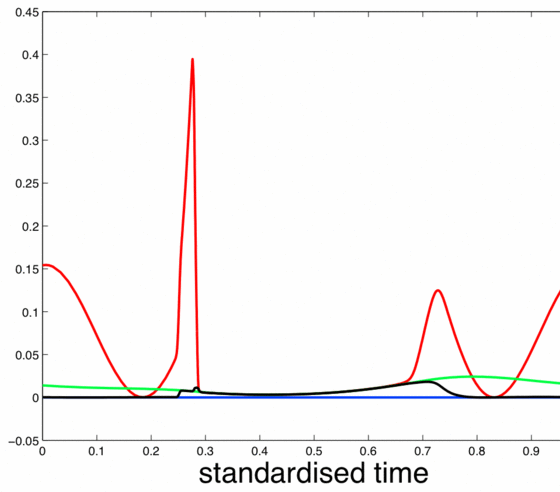
Results of simulation for random capacitance
People in group
- R. Pulch
Ongoing projects
- none
Cooperation
- Prof. P. Rentrop (TU Munich)
- Prof. D. Xiu (Purdue University, Indiana, USA)
Literature / Selected Publications:
- F. Augustin, A. Gilg, M. Paffrath, P. Rentrop, U. Wever: Polynomial chaos for the approximation of uncertainties: chances and limits. Euro. Jnl. of Applied Mathematics 19 (2008), pp. 149-190.
- R.G. Ghanem, P.D. Spanos: Stochastic Finite Elements. (rev. ed.) Dover Publications Inc., Mineola, New York, 2003.
- R. Pulch: Polynomial chaos for multirate partial differential algebraic equations with random parameters. Appl. Numer. Math. 59:10 (2009), pp. 2610-2624.
- R. Pulch, C. van Emmerich: Polynomial chaos for simulating random volatilities. Mathematics and Computers in Simulation 80 (2009), pp. 245-255.
- D. Xiu: Numerical Methods for Stochastic Computations. Princeton University Press, New Jersey, 2010.
