Dynamic Iteration Schemes
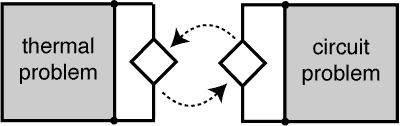
Dynamic iteration via source coupling
Standard time-integration methods solve transient problems all at once. This may become very inefficient or impossible for large systems of equations. Imaging that such large systems often stem from a coupled problem formulation, where different physical phenomena interact and need to be coupled in order to produce a precise mathematical model.
E.g. highly integrated electric circuits (as in memory chips or CPUs) produce heat, which effects in turn their behavior as electrical system; thus one needs to couple electric and thermal subproblem descriptions. On the one hand, this creates multiple time scales due to different physical phenomena, which demands an efficient treatment, see multirate. On the other hand, in a professional environment one usually has dedicated solvers for the subproblems, which need to be used, and an overall problem formulation is not feasible for any of the involved tools.
For those partitioned problems a dynamic iteration method becomes beneficial or even the sole way-out: it keeps the subproblems separate, solves subproblems sequentially (or in parallel) and iterates until convergence (fixed-point interation). Thus the subproblem's structure can be exploited in the respective integration.
To guarantee or to speed up convergence the time interval of interest is split into a series of windows. Then the time-integration of the windows is applied sequentially and in each window the subproblems are solved iteratively by your favoured method.
Group members working on that field
- Andreas Bartel
- Michael Günther
Former and ongoing Projects
- CoMSON
- ICESTARS
Cooperation
- Herbert De Gersem, Katholieke Universiteit Leuven
