Coupled DAE Problems
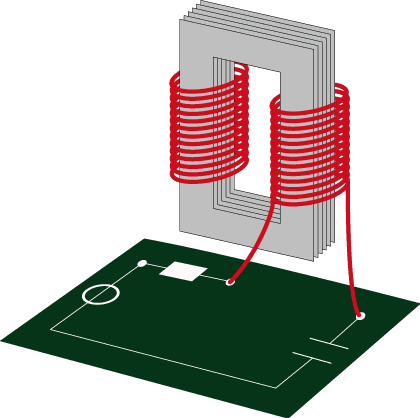
A circuit (DAE model) coupled to a magnetostatic field device (PDE model)
Coupled Problems of differential-algebraic equations (DAEs) arise typically from either multiphysical modeling (e.g. in circuit simulation with heating) or from refined modeling, where crucial parts of the original problem are replaced by a better, but computational more expensive model (e.g. circuits refined by field models). Furthermore splitting methods may turn a monolithic DAE problem into coupled subproblems, e.g. because of different time scales (multirate). In any case the DAEs arise from network approaches or space-discretization of PDAEs (Partial Differential Algebraic Equations).
Often the coupled equations have quite different properties, i.e., symmetries, definiteness or time scales. Thus the coupled system must be analyzed (e.g. the index) and tailored methods have to be developed (e.g. dynamic iteration).
Details
Publications
- 2016
3418.
Teng, Long; Ehrhardt, Matthias; Günther, Michael
Modelling stochastic correlation with modified Ornstein-Uhlenbeck process
Progress in Industrial Mathematics at ECMI 2014, Page 113–120
Springer Heidelberg
Publisher: Springer Cham
20163417.
Teng, Long; Ehrhardt, Matthias; Günther, Michael
Modelling stochastic correlation with modified Ornstein-Uhlenbeck process
Progress in Industrial Mathematics at ECMI 2014, Page 113–120
Springer Heidelberg
Publisher: Springer Cham
20163416.
Teng, Long; Ehrhardt, Matthias; Günther, Michael
Modelling stochastic correlation with modified Ornstein-Uhlenbeck process
Progress in Industrial Mathematics at ECMI 2014, Page 113–120
Springer Heidelberg
Publisher: Springer Cham
20163415.
Hoffmann, Heiko; Tausch, Michael W.
Modellreaktionen mit Sonnenlicht oder Taschenlampe
Nachrichten aus der Chemie, 64 (11) :1090--1093
2016
Publisher: Wiley3414.
Kossaczk{\'{y}}, I.; Ehrhardt, M.; Günther, M.
Modifications of the {PCPT} method for {HJB} equations
Publisher: Author(s)
20163413.
Modifications of the PCPT method for HJB equations
, AIP Conference ProceedingsVolume1773, Page 030002
AIP Publishing LLC
20163412.
Kossaczkỳ, I; Ehrhardt, Matthias; Günther, Michael
Modifications of the PCPT method for HJB equations
, 8th International Conference for Promoting the Application of Mathematics in Technical and Natural Sciences - AMiTaNS’16Volume1773, Page 030002
Publisher: American Institute of Physics
20163411.
Kossaczkỳ, I; Ehrhardt, Matthias; Günther, Michael
Modifications of the PCPT method for HJB equations
, 8th International Conference for Promoting the Application of Mathematics in Technical and Natural Sciences - AMiTaNS’16Volume1773, Page 030002
Publisher: American Institute of Physics
20163410.
Kossaczkỳ, I; Ehrhardt, Matthias; Günther, Michael
Modifications of the PCPT method for HJB equations
, 8th International Conference for Promoting the Application of Mathematics in Technical and Natural Sciences - AMiTaNS’16Volume1773, Page 030002
Publisher: American Institute of Physics
20163409.
Schweitzer, Marcel
Monotone convergence of the extended Krylov subspace method for Laplace-Stieltjes functions of Hermitian positive definite matrices
Linear Algebra Appl., 507 :486-498
20163408.
Schweitzer, Marcel
Monotone convergence of the extended Krylov subspace method for Laplace-Stieltjes functions of Hermitian positive definite matrices
Linear Algebra Appl., 507 :486-498
20163407.
Schweitzer, Marcel
Monotone convergence of the extended Krylov subspace method for Laplace-Stieltjes functions of Hermitian positive definite matrices
Linear Algebra Appl., 507 :486-498
20163406.
Knechtli, Francesco; Günther, Michael; Peardon, Michael
Monte Carlo methods
from SpringerBriefs in Physics
Page 35–53
Publisher: Springer Netherlands
2016
35–533405.
Knechtli, Francesco; Günther, Michael; Peardon, Michael
Monte Carlo methods
from SpringerBriefs in Physics
Page 35–53
Publisher: Springer Netherlands
2016
35–533404.
Frobel, Dominique-Jacqueline
Moose und Flechten an ausgewählten Plätzen im Stadtgebiet von Wuppertal
20163403.
Bolten, Matthias; Kahl, K.; Sokolović, S.
Multigrid methods for Tensor structured Markov chains with low rank approximation
SIAM J. Sci. Comput., 38 (2) :A649-A667
20163402.
Bolten, M.; Kahl, K.; Sokolović, S.
Multigrid methods for Tensor structured Markov chains with low rank approximation
SIAM J. Sci. Comput., 38 (2) :A649-A667
20163401.
Bolten, M.; Kahl, K.; Sokolović, S.
Multigrid methods for Tensor structured Markov chains with low rank approximation
SIAM J. Sci. Comput., 38 (2) :A649--A667
20163400.
Günther, Michael; Hachtel, Christoph; Sandu, Adrian
Multirate {GARK} Schemes for Multiphysics Problems
Scientific Computing in Electrical Engineering
Page 115--121
Publisher: Springer International Publishing
2016
115--1213399.
Hachtel, Christoph; Kerler-Back, Johanna; Bartel, Andreas; Günther, Michael; Stykel, Tatjana
Multirate DAE/ODE-Simulation and Model Order Reduction for Coupled Circuit-Field Systems
20163398.
Günther, Michael; Hachtel, Christoph; Sandu, Adrian
Multirate GARK schemes for multiphysics problems
In Bartel, Andreas and Clemens, Markus and Günther, Michael and ter Maten, E. Jan W., Editor, Scientific Computing in Electrical Engineering: SCEE 2014, Wuppertal, Germany, July 2014fromMathematics in Industry, Page 115–121
In Bartel, Andreas and Clemens, Markus and Günther, Michael and ter Maten, E. Jan W., Editor
Publisher: Springer Cham
20163397.
Günther, Michael; Hachtel, Christoph; Sandu, Adrian
Multirate GARK schemes for multiphysics problems
In Bartel, Andreas and Clemens, Markus and Günther, Michael and ter Maten, E. Jan W., Editor, Scientific Computing in Electrical Engineering: SCEE 2014, Wuppertal, Germany, July 2014fromMathematics in Industry, Page 115–121
In Bartel, Andreas and Clemens, Markus and Günther, Michael and ter Maten, E. Jan W., Editor
Publisher: Springer Cham
20163396.
Bartel, Andreas; Günther, Michael; Hachtel, Christoph; Sandu, Adrian
Multirate GARK schemes for multiphysics problems
:115--121
20163395.
Günther, Michael; Sandu, Adrian
Multirate generalized additive Runge Kutta methods
Numerische Mathematik, 133 (3) :497–524
2016
Publisher: Springer New York3394.
Günther, Michael; Sandu, Adrian
Multirate generalized additive Runge Kutta methods
Numerische Mathematik, 133 (3) :497–524
2016
Publisher: Springer New York
