Multirate
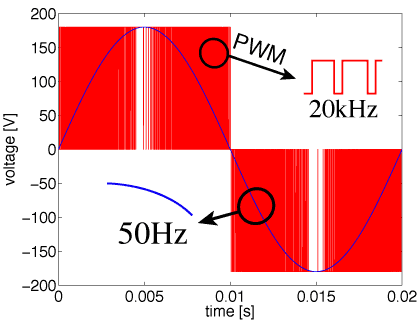
Highly integrated electric cicuits show a phenomenon called latency. That is, a processed signal causes activity only in a small subset of the whole circuit (imagine a central processing unit), whereas the other part of the system behaves almost constant over some time - is latent. Such an electric system can be described as coupled system, where the waveforms show different time scales, also refered to as multirate.
More generally, any coupled problem formulation due to coupled physical effects, may cause a multirate problem: image the simulation of car driving on the road, there you need a model for the wheel, the chassis, the dampers, the road,... (cf. co-simulation). Again each system is covered by their own time constant, which might vary over several orders of magnitude comparing different subsystems.
Classical methods cannot exploit this multirate potential, but resolve everything on the finest scale. This causes an over sampling of the latent components. In constrast, Co-simulation or especially dedicated multirate methods are designed to use the inherent step size to resolve the time-domain behaviour of each subystem with the required accuracy. This requires a time-stepping for each.
Group members working in that field
- Andreas Bartel
- Michael Günther
Former and ongoing Projects
- CoMSON
- ICESTARS
- 03GUNAVN
Cooperations
- Herbert de Gersem, K.U. Leuven, Belgium
- Jan ter Maten, TU Eindhoven and NXP, the Netherlands
Publications
- 2020
4341.
Hutzenthaler, Martin; Jentzen, Arnulf; Kruse, Thomas; Nguyen, Tuan Anh
A proof that rectified deep neural networks overcome the curse of dimensionality in the numerical approximation of semilinear heat equations
SN Partial Differential Equations and Applications, 1 (2) :1–34
2020
Publisher: Springer International Publishing4340.
Aab, Alexander; others
A Search for Ultra-high-energy Neutrinos from TXS 0506+056 Using the Pierre Auger Observatory
Astrophys. J., 902 (2) :105
20204339.
Kühn, J.; Bartel, A.; Putek, P.
A Thermal Extension of Tellinen's Scalar Hysteresis Model
, Scientific Computing in Electrical Engineering SCEE 2018VolumeXfromMathematics in Industry
Publisher: Springer, Berlin
20204338.
Kühn, Jan; Bartel, Andreas; Putek, Piotr
A thermal extension of Tellinen’s scalar hysteresis model
In Nicosia, Giuseppe and Romano, Vittorio, Editor, Scientific Computing in Electrical Engineering: SCEE 2018, Taormina, Italy, September 2018fromMathematics in Industry, Page 55–63
In Nicosia, Giuseppe and Romano, Vittorio, Editor
Publisher: Springer Cham
20204337.
Kruse, Thomas; Schneider, Judith C; Schweizer, Nikolaus
A toolkit for robust risk assessment using F-divergences
Management Science
2020
Publisher: INFORMS Inst. for Operations Res. and the Management Sciences4336.
Kruse, Thomas; Schneider, Judith; Schweizer, Nikolaus
A toolkit for robust risk assessment using F-divergences
Management Science, 67 (10)
2020
Publisher: INFORMS4335.
Wolf, Julian; Huber, Florian; Erochok, Nikita; Heinen, Flemming; Guérin, Vincent; Legault, Claude Y.; Kirsch, Stefan F.; Huber, Stefan M.
Activation of a Metal‐Halogen Bond by Halogen Bonding
Angewandte Chemie International Edition, 59 (38) :16496–16500
2020
ISSN: 1433-7851, 1521-37734334.
Glück, Jochen; Weber, Martin R.
Almost interior points in ordered Banach spaces and the long-term behaviour of strongly positive operator semigroups
Studia Math., 254 (3) :237--263
20204333.
[german] Zeller, Diana; Bohrmann-Linde, Claudia
Alternative Solarzellen mit Titandioxid - Ein Mentoring Projekt
MNU, 73 (2) :108--112
20204332.
Totzeck, Claudia
An anisotropic interaction model with collision avoidance
Kinetic and Related Models, 13 (6) :1219-1242
20204331.
Kruse, Thomas; Urusov, Mikhail
Approximating exit times of continuous Markov processes
Discrete and Continuous Dynamical Systems-B, 25 (9) :3631–3650
2020
Publisher: American Institute of Mathematical Sciences4330.
[german] Grandrath, Rebecca; Bohrmann-Linde, Claudia
BNE-Strukturen gemeinsam gestalten. Fachdidaktische Perspektiven und Forschungen zu Bildung für nachhaltige Entwicklung in der Lehrkräftebildung.
Volume 13 from Erziehungswissenschaft und Weltgesellschaft
Chapter Chemiedidaktik als BNE-Multiplikator - Arbeitskreispraktika zur Erprobung von Schulversuchen und deren Reflexion hinsichtlich des BNE-Bezug., Page 83-94
Publisher: Andreas Keil, Miriam Kuckuck und Mira Faßbender, Waxman, Münster
2020
83-94ISBN: 978-3-8309-4158-3
4329.
Bohrmann-Linde, Claudia; Kröger, Simone; Siehr (Hrsg.), Ilona
Chemie 2 - Gymnasium G9 NRW
Publisher: C.C.Buchner
20204328.
Bohrmann-Linde, Claudia; Kröger, Simone; Siehr (Hrsg.), Ilona
Chemie Gesamtband Sek I NRW
Publisher: C.C.Buchner
20204327.
Tausch, Michael W.
Chemie mit Licht - Innovative Didaktik für Studium und Lehre
Publisher: Springer Verlag
2020ISBN: 978-3-662-60376-5
4326.
Tiemann, Myrel; Clemens, Markus; Schmuelling, Benedikt
Comparison of Conventional and Magnetizable Concrete Core Designs in Wireless Power Transfer for Electric Vehicles
2020 {IEEE} {PELS} Workshop on Emerging Technologies: Wireless Power Transfer ({WoW})
Publisher: {IEEE}
November 20204325.
Totzeck, Claudia; Wolfram, Marie-Therese
Consensus-Based Global Optimization with Personal Best
Mathematical Biosciences and Engineering, 17 (5) :6026-6044
20204324.
Günther, Michael; Höllwiesera, Roman; Knechtli, Francesco
Constrained HMC algorithms for Gauge-Higgs models
, AIP Conference ProceedingsVolume2293, Page 290004
AIP Publishing LLC
20204323.
Günther, Michael; Höllwieser, Roman; Knechtli, Francesco
Constrained hybrid Monte Carlo algorithms for Gauge-Higgs models
Computer Physics Communications, 254 :107192
2020
Publisher: Elsevier4322.
Günther, Michael; Höllwieser, Roman; Knechtli, Francesco
Constrained hybrid Monte Carlo algorithms for Gauge-Higgs models
Computer Physics Communications, 254 :107192
2020
Publisher: Elsevier4321.
Günther, Michael; Höllwieser, Roman; Knechtli, Francesco
Constrained hybrid Monte Carlo algorithms for gauge-Higgs models
Computer Physics Communications, 254 :107192
2020
Publisher: North-Holland4320.
De Sterck, H.; Friedhoff, S.; Howse, A. J. M.; MacLachlan, S. P.
Convergence analysis for parallel-in-time solution of hyperbolic systems
Numer. Linear Algebra Appl., 27 (1) :e2271, 31
20204319.
De Sterck, H.; Friedhoff, S.; Howse, A. J. M.; MacLachlan, S. P.
Convergence analysis for parallel-in-time solution of hyperbolic systems
Numer. Linear Algebra Appl., 27 (1) :e2271, 31
20204318.
De Sterck, H.; Friedhoff, S.; Howse, A. J. M.; MacLachlan, S. P.
Convergence analysis for parallel-in-time solution of hyperbolic systems
Numer. Linear Algebra Appl., 27 (1) :e2271, 31
20204317.
Abel, Ulrich; Heilmann, Margareta; Kushnirevych, Vitaliy
Convergence of linking Baskakov-type operators
Periodica Mathematica Hungarica, 80 :280-288
2020
