Multirate
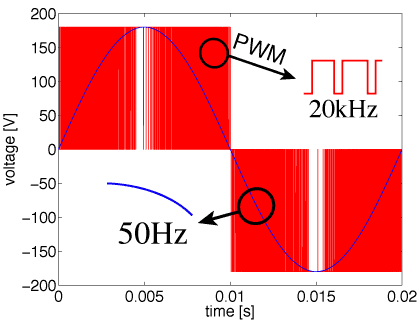
Highly integrated electric cicuits show a phenomenon called latency. That is, a processed signal causes activity only in a small subset of the whole circuit (imagine a central processing unit), whereas the other part of the system behaves almost constant over some time - is latent. Such an electric system can be described as coupled system, where the waveforms show different time scales, also refered to as multirate.
More generally, any coupled problem formulation due to coupled physical effects, may cause a multirate problem: image the simulation of car driving on the road, there you need a model for the wheel, the chassis, the dampers, the road,... (cf. co-simulation). Again each system is covered by their own time constant, which might vary over several orders of magnitude comparing different subsystems.
Classical methods cannot exploit this multirate potential, but resolve everything on the finest scale. This causes an over sampling of the latent components. In constrast, Co-simulation or especially dedicated multirate methods are designed to use the inherent step size to resolve the time-domain behaviour of each subystem with the required accuracy. This requires a time-stepping for each.
Group members working in that field
- Andreas Bartel
- Michael Günther
Former and ongoing Projects
- CoMSON
- ICESTARS
- 03GUNAVN
Cooperations
- Herbert de Gersem, K.U. Leuven, Belgium
- Jan ter Maten, TU Eindhoven and NXP, the Netherlands
Publications
- 2021
4489.
Donatelli, Marco; Ferrari, Paola; Furci, Isabella; Serra-Capizzano, Stefano; Sesana, Debora
Multigrid methods for block-Toeplitz linear systems: convergence analysis and applications
Numer. Linear Algebra Appl., 28 (4) :Paper No. e2356, 20
2021
ISSN: 1070-53254488.
Hutzenthaler, Martin; Jentzen, Arnulf; Kruse, Thomas; others
Multilevel Picard iterations for solving smooth semilinear parabolic heat equations
Partial Differential Equations and Applications, 2 (6) :1--31
2021
Publisher: Springer4487.
Hutzenthaler, Martin; Jentzen, Arnulf; Kruse, Thomas; others
Multilevel Picard iterations for solving smooth semilinear parabolic heat equations
Partial Differential Equations and Applications, 2 (6) :1–31
2021
Publisher: Springer International Publishing4486.
Ferrari, Paola; Furci, Isabella; Serra-Capizzano, Stefano
Multilevel symmetrized Toeplitz structures and spectral distribution results for the related matrix sequences
Electron. J. Linear Algebra, 37 :370-386
20214485.
Ferrari, Paola; Furci, Isabella; Serra-Capizzano, Stefano
Multilevel symmetrized Toeplitz structures and spectral distribution results for the related matrix sequences
Electron. J. Linear Algebra, 37 :370-386
20214484.
Ferrari, Paola; Furci, Isabella; Serra-Capizzano, Stefano
Multilevel symmetrized Toeplitz structures and spectral distribution results for the related matrix sequences
Electron. J. Linear Algebra, 37 :370-386
20214483.
Hachtel, Christoph; Bartel, Andreas; Günther, Michael; Sandu, Adrian
Multirate implicit Euler schemes for a class of differential--algebraic equations of index-1
Journal of Computational and Applied Mathematics, 387 :112499
2021
Publisher: North-Holland4482.
Hachtel, Christoph; Bartel, Andreas; Günther, Michael; Sandu, Adrian
Multirate implicit Euler schemes for a class of differential-algebraic equations of index-1
Journal of Computational and Applied Mathematics, 387 :112499
2021
Publisher: North-Holland4481.
Hachtel, Christoph; Bartel, Andreas; Günther, Michael; Sandu, Adrian
Multirate implicit Euler schemes for a class of differential-algebraic equations of index-1
Journal of Computational and Applied Mathematics, 387 :112499
2021
Publisher: North-Holland4480.
Günther, Michael; Sandu, Adrian
Multirate linearly-implicit GARK schemes
BIT Numerical Mathematics :1--33
2021
Publisher: Springer Netherlands4479.
Lübke, Marco
Neuartige multifunktionelle Tenside auf Basis nachwachsender Rohstoffe
20214478.
Claus, L.; Bolten, Matthias
Non-overlapping block smoothers for the Stokes equations
Num. Lin. Alg. Appl., 28 (6) :e2389
20214477.
Claus, L.; Bolten, M.
Non-overlapping block smoothers for the Stokes equations
Num. Lin. Alg. Appl., 28 (6) :e2389
20214476.
Claus, L.; Bolten, M.
Non-overlapping block smoothers for the Stokes equations
Num. Lin. Alg. Appl., 28 (6) :e2389
20214475.
Eichfelder, Gabriele; Klamroth, Kathrin; Niebling, Julia
Nonconvex constrained optimization by a filtering branch and bound
Journal of Global Optimization, 80 :31-61
20214474.
Mironchenko, Andrii; Kawan, Christoph; Glück, Jochen
Nonlinear small-gain theorems for input-to-state stability of infinite interconnections
Math. Control Signals Systems, 33 (4) :573--615
20214473.
Krämer, Veronika; Barwari, Beawer; Burgmann, Sebastian; Rohde, Martin; Rentschler, Simon; Holzknecht, Christopher; Gmelin, Christoph; Janoske, Uwe
Numerical analysis of an adhering droplet applying an adapted feedback deceleration technique
International Journal of Multiphase Flow, 145 :103808
December 2021
Publisher: Elsevier {BV}4472.
Jacob, Birgit; Zwart, Hans
Observability for port-Hamiltonian systems
European Control Conference (ECC) :2052-2057
20214471.
Markert, Clara; Thinius, Marco; Lehmann, Laura; Heintz, Chris; Stappert, Florian; Wissdorf, Walter; Kersten, Hendrik; Benter, Thorsten; Schneider, Bradley B.; Covey, Thomas R.
Observation of charged droplets from electrospray ionization (ESI) plumes in API mass spectrometers
Analytical and Bioanalytical Chemistry
July 2021
ISSN: 1618-2642, 1618-26504470.
Friedhoff, S.; Southworth, B. S.
On "optimal" $h$-independent convergence of parareal and multigrid-reduction-in-time using Runge-Kutta time integration
Numer. Linear Algebra Appl., 28 (3)
20214469.
Friedhoff, S.; Southworth, B. S.
On "optimal" $h$-independent convergence of parareal and multigrid-reduction-in-time using Runge-Kutta time integration
Numer. Linear Algebra Appl., 28 (3) :Paper No. e2301, 30
20214468.
Friedhoff, S.; Southworth, B. S.
On "optimal" $h$-independent convergence of parareal and multigrid-reduction-in-time using Runge-Kutta time integration
Numer. Linear Algebra Appl., 28 (3) :Paper No. e2301, 30
20214467.
Farkas, Bálint; Friesen, Martin; Rüdiger, Barbara; Schroers, Dennis
On a class of stochastic partial differential equations with multiple invariant measures
NoDEA
20214466.
Glück, Jochen
On disjointness, bands and projections in partially ordered vector spaces
Positivity and its applications from Trends Math.
Page 141--171
Publisher: Birkhäuser/Springer, Cham
2021
141--1714465.
Glück, Jochen
On the decoupled Markov group conjecture
Bull. Lond. Math. Soc., 53 (1) :240--247
2021
